Here we present several paradoxes regarding environmental emissions in supernetworks, in which certain links correspond to telecommunication links and are characterized by a zero emission factor. By a zero emission factor, we mean that, irregardless of  the flow on such links the total emissions generated by the use of such links is zero.

We identify three distinct paradoxical phenomena that can occur in such networks, which demonstrate that so-called improvements to the network may result in increases in total emissions generated. These paradoxes were discovered by Nagurney and Dong and published in a paper in the journal Transportation Research D in 2001.

Paradox 1: The Addition of a Zero Emission Link Results in an Increase in Total Emissions with No Change in Demand

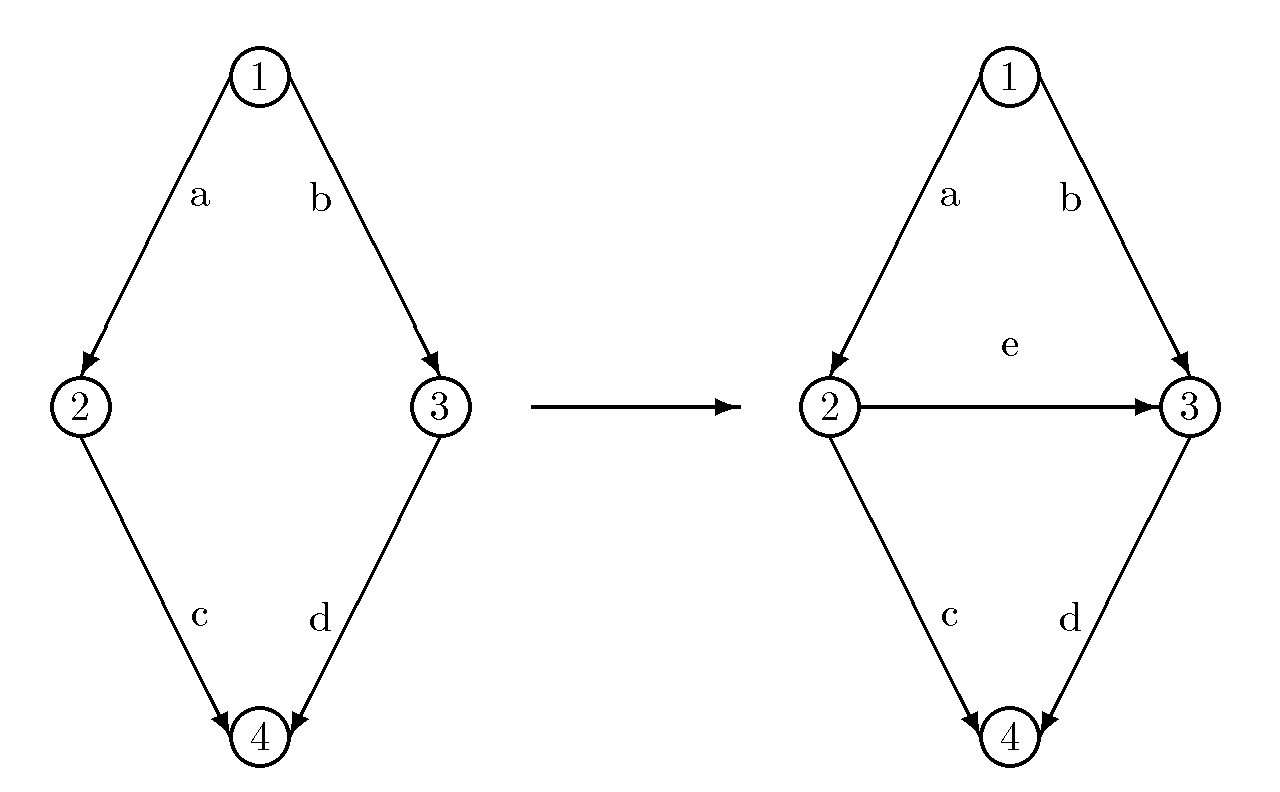
We first consider the network below which has the Braess (1968) network topology and user link cost structure.

There are 4 links: a, b, c, d; 4 nodes: 1, 2, 3, 4, and a single origin/destination pair of nodes (1,4) in the first network. There are, thus, 2 paths available to users between this O/D pair: p₁=(a,c) and p₂=(b,d). The user link cost functions are: c_a(f_a)=10f_a, c_b(f_b)=f_b+50, c_c(f_c)=f_c+50, c_d(f_d)=10f_d, where f_a denotes the flow on link a, f_b denotes the flow on link b, and so on.

The demand for the origin/destination pair is given by d_w=6. Assume that the emission factors on the links are given by: h_a=.2, h_b=.1, h_c=.1, and h_d=.2. This means that the total emissions generated on link a, given a flow of f_a on it would be h_af_a, and so on, for the other links.

The user-optimized flow pattern, under which the network is in equilibrium with no user or traveller having any incentive to alter his travel path, is given by: x_p1*=3, x_p2*=3, with equilibrium link flows: f_a*=3, f_b*=3, f_c*=3, f_d*=3, and with associated equilibrium path costs: C_p1=83 and C_p2=83. The total emissions generated by the equilibrium link flow pattern is: E=.2(3)+.1(3)+.1(3)+.2(3)=1.8.

Now, as illustrated in the figure above, consider the addition of a new link e, joining node 2 to node 3 to the original network. Assume that link e has an emission factor h_e=0 and a user cost function associated with traveling on link e given by c_e(f_e)=f_e+10. The addition of this link creates a new path p₃=(a,e,d) that is available to the users of the network. Assume also that the demand d_w remains unchanged at 6 units of flow.

The equilibrium path flow pattern on the new network is: x_p1**=2, x_p2**=2, x_p3**=2, with equilibrium link flows: f_a**=4, f_b**=2, f_c**=2, f_e**=2, f_d**=4, and with associated equilibrium path costs: C_p1=C_p2=C_p3=92.

The total emissions generated in the new network are equal to 2, a value greater than the total generated in the original network. Hence, the addition of a new link with zero emissions makes not only everyone worse off in terms of cost but also in terms of the emissions generated.
 

Paradox 2 - A Decrease in Demand on a Supernetwork with a Zero Emission Link May Result in an Increase in Emissions

We now illustrate a second paradox regarding a supernetwork with a zero emission link in which a decrease in the demand for an origin/destination pair, joined by a single path consisting of a single link with a zero emission factor, results in an increase in total emissions.

Consider the supernetwork depicted in the Figure below. The user link cost functions are: c_a(f_a)=f_a+1, c_b(f_b)=f_b+4, and c_c(f_c)=f_c+1. There are two origin/destination pairs: w₁=(1,2) and w₂=(1,3). The path connecting O/D pair w₁, p₁, consists of the single link a. The paths connecting O/D pair w₂ are: p₂=(a,c) and p₃=b. The demands in the original problem are: d_w1=1 and d_w2=2. The emission factors on the links are: h_a=0., h_b=.01, and h_c=.5. Hence, link a may correspond to a telecommunication link.

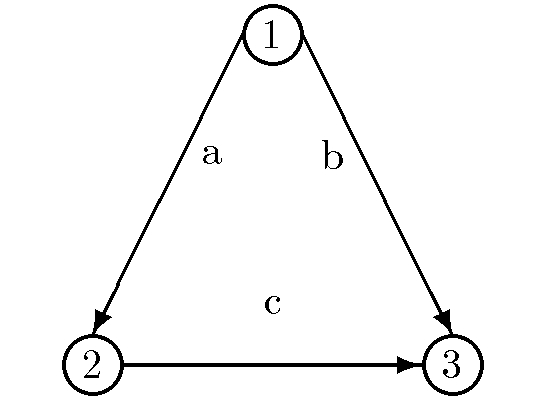
The network equilibrium path flow pattern is: x_p1*=1, x_p2*=1, x_p3*=1, with induced link flow pattern: f_a*=2, f_b*=f_c*=1. The path user costs are: For O/D pair w₁: C_p1=3, and for origin/destination (O/D) pair w₂: C_p2=C_p3=5. The total emissions generated: E=.02+.01+.5=.51.

We now consider a decrease in demand associated with O/D pair w₁ with the new demand d_w1=.5 and all other data remain the same. The new network equilibrium path flow pattern is: x_p1**=.5, x_p2**=1.1666..., x_p3**=.833..., with induced equilibrium link flow pattern: f_a**=1.666..., f_b**=.833..., f_c**=1.166... The new path user costs are: For O/D pair w₁: C_p1=2.666..., and for O/D pair w2: C_p2=C_p3=4.833.... The total emissions now generated: E=0.000...+.00833...+.5830=.59133....

Hence, the total emissions have increased from .51 to .59133... even though the demand has decreased. Moreover, the costs for paths between the two origin/destination pairs have decreased.

Paradox 3 - Adding A New Path which Consists Solely of a Zero Emission Link and which Shares No Links With Any Other Path May Result in an Increase in Emissions

We now illustrate a third paradox regarding a supernetwork in which the addition of a new path consisting solely of a zero emission links results in an increase in total emissions.

Consider the first network depicted in the Figure below. The user link cost functions are: c_a(f_a)=f_a+10, c_b(f_b)=3f_a+3f_b. There is a single origin/destination pair: w₁=(1,2). The paths connecting the O/D pair are: p₁=a and p₂=b. The demands in this network is: d_w1=5. The emission factors on the links are: h_a=0.1, h_b=.5.

The network equilibrium path flow pattern is: x_p1*=5, x_p2*=0, with induced link flow pattern: f_a*=5, f_b*=0. The path user costs are: C_p1=15, and C_p2=15. The total emissions generated E*=.5+0=.5.

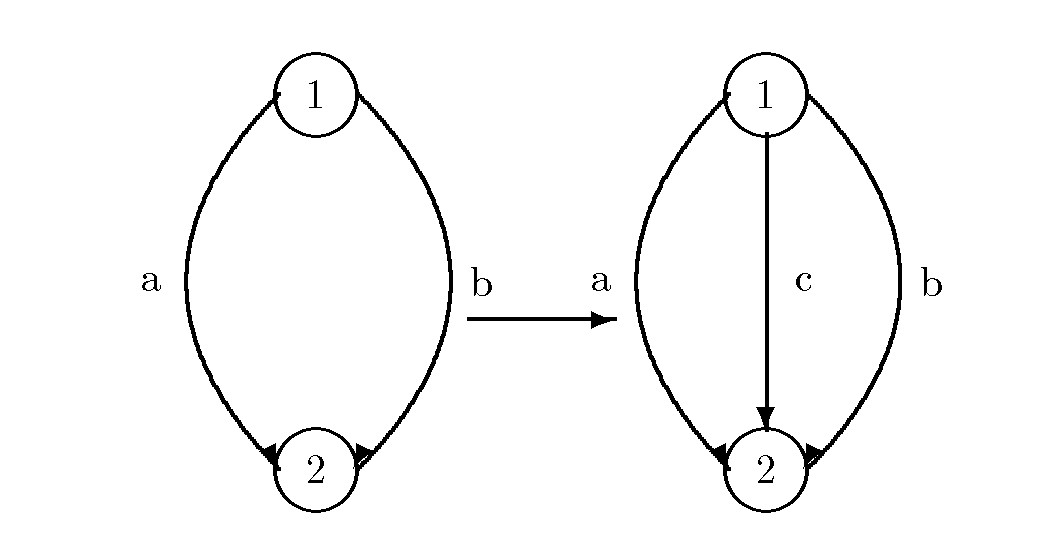
The new network equilibrium link flow pattern is: f_a**=2, f_b**=2, and f_c**=1. The user path travel costs are: C_p1=C_p2=C_p3=12. The total emissions now generated are given by: E=0.2 + 1.0+0.0=1.2. Hence, the equilibrium path costs have decreased. However, the total emissions have increased from .5 to 1.2 even though a new disjoint path (that is, a path that has no links in common with any other path) with zero emissions was added.